배심원 다수의 결정으로 피고인이 유죄라고 (또는 무죄라고) 평결을 내린 상황을 가정해 보자.[역주1] 그들이 올바른 평결에 도달했을 가능성은 얼마나 될까?
프랑스 철학자 콩도르세(Marquis de Condorcet, 1743-1794)는 이 문제에 대해 수학적으로 정확한 답을 얻을 수 있음을 보여 주었다. 이것은 “콩도르세의 배심원 정리”(Condorcet Jury Theorem)로 알려져 있다.[1]
그러나 콩도르세의 정리는 단지 배심원에 관한 것만은 아니다. 이것은 집단적 의사 결정 일반에 대한 것이다. 따라서 일부 철학자들은 이 정리를 민주적 정부 형태를 지지하는 논거로 사용해 왔다.
이 글은 콩도르세의 정리를 소개하고, 철학자들이 이것을 어떻게 민주주의를 지지하는 논증으로 사용해 왔는지에 대해 설명한다.
1. 콩도르세의 배심원 정리
콩도르세의 정리는 몇 가지 가정에 의존한다.
첫째, 배심원들이 독립적으로 판단한다는 것이다. 즉, 그들은 각자 증거를 검토하고 스스로 결정을 내린다.
둘째, 배심원들이 유능하다는 것이다. 이는 그들 각각이 올바른 평결을 내릴 가능성이 그렇지 않을 가능성보다 높다는 것을 의미한다. 우리는 50%를 넘는 어떤 확률이든 선택할 수 있으므로, 여기에서는 각 배심원이 올바른 평결을 내릴 확률이 60%라고 가정해 보자.
이러한 가정들을 토대로 우리는 배심원 다수가 올바른 평결을 내릴 확률을 계산할 수 있다.[2]
배심원이 한 명인 경우, 올바른 평결을 내릴 확률은 60%이다. 배심원이 세 명이라면, 다수가 올바른 평결을 내릴 확률은 64.8%로 높아진다.
이것은 어떻게 계산되는 것일까? 다수가 올바른 평결을 내리는 네 가지 가능한 방식이 있다. 이 경우들은 상호 배타적이기 때문에, 각 경우에 대한 확률을 구해 그것들을 더함으로써 이 네 가지 경우 중 하나가 일어날 확률[역주2]을 구할 수 있다.[3]
경우 1: 배심원 1과 2는 올바른 판단을 내리고 배심원 3은 잘못된 판단을 내리는 경우, 60% × 60% × 40% = 14.4%
경우 2: 배심원 1과 3은 올바른 판단을 내리고 배심원 2는 잘못된 판단을 내리는 경우, 60% × 40% × 60% = 14.4%
경우 3: 배심원 2와 3은 올바른 판단을 내리고 배심원 1은 잘못된 판단을 내리는 경우, 40% × 60% × 60% = 14.4%
경우 4: 모든 배심원이 올바른 판단을 내리는 경우, 60% × 60% × 60% = 21.6%
이 확률들을 모두 더하면 64.8%가 된다.[4]
여기서 주목할 점은 한 명의 배심원이 있을 때보다 세 명의 배심원이 있을 때 올바른 평결을 내릴 확률이 높다는 사실이다. 배심원의 수가 많아질수록 다수가 올바른 평결을 내릴 가능성도 높아진다. 배심원이 25명이라면, 다수가 올바른 평결을 내릴 확률은 무려 84.6%까지 높아진다![5] 실제로 각 배심원이 올바른 평결을 내릴 확률이 50%를 넘기만 한다면, 배심원 수를 늘릴수록 다수가 올바른 평결에 도달할 확률은 100%에 가까워진다.[6]
2. 민주주의 옹호 논증으로서의 배심원 정리
콩도르세의 배심원 정리와 이상적인 민주주의에서 시민들의 투표 행동 사이에는 많은 유사점이 있다. 이러한 유사성 때문에 철학자들은 민주주의가 최선의 공직 선거 후보자와 정책을 선택하는 데 효과적이라는 주장을 뒷받침하기 위해 이 정리를 활용해 왔다.
첫째, 배심원들이 각자 평결을 내리는 것과 마찬가지로, 민주주의에서 유권자들은 각자 독립적으로 투표 결정을 한다. 많은 경우 이는 비밀 투표를 통해 이루어진다.
둘째, 법정에서는 변호사들이 배심원들에게 증거를 제시하고, 민주주의에서는 공공 기관들이 유권자들이 좋은 결정을 내리도록 돕기 위한 조치를 취한다. 학교는 학생들에게 정부 제도에 대해 가르치고, 뉴스 매체는 시민들에게 공직 선거 후보자와 정책에 대한 정보를 제공한다. 따라서 이상적인 민주주의에서는 유권자들이 유능하고 충분한 정보를 갖추고 있어, 최선의 정치인과 정책을 선택할 확률이 50%를 넘는다.
그런데 배심원 제도와 민주주의 사이에는 중요한 차이점이 있다. 그것은 투표에는 매우 많은 수의 시민들이 참여한다는 것이다. 작은 국가에도 25명의 배심원보다는 훨씬 더 많은 유권자들이 있으므로, 콩도르세의 가정이 모두 성립한다면 민주주의는 다수결로 거의 항상 최선의 공직 선거 후보자를 선택할 것이다.[7]
3. 비판
하지만 현실적으로, 대부분의 사람들은 민주주의가 종종 최선의 선택을 하지 못한다고 생각한다. 이것은 민주주의를 지지하는 이 논증이 완전히 실패했다는 것을 의미하는가?
그렇지는 않다. 하지만 이는 콩도르세의 배심원 정리와 실제 민주주의 투표 사이의 차이점을 더 면밀히 살펴서, 보다 약화된 주장을 하는[역주 3] 유사한 논증이 여전히 유효할 수 있는지 따져볼 필요가 있음을 보여 준다.
첫째, 배심원의 경우에는 유죄 또는 무죄, 올바른 평결과 잘못된 평결이 명확히 나뉜다. 반면 투표에서의 선택은 단순히 옳고 그름의 문제가 아니다. 특정 공직선거 후보자나 정책은 덜 효과적일 수 있지만, 그것들은 유죄 평결이 그런 것과 같은 방식으로 ‘올바르거나’ ‘잘못된’ 것이라 할 수는 없다.
이러한 차이점은 보완이 가능하다. 우리는 유권자들이 단지 올바르거나 잘못된 후보자와 정책을 선택하는 것이 아니라, 더 좋거나 나쁜 것들을 선택하는 것으로 생각할 수 있다. 만약 유권자들이 최선의 것을 선택할 가능성이 그렇지 않을 가능성보다 높다면, 우리는 여전히 콩도르세의 배심원 정리를 민주주의에 적용할 수 있다.[8]
둘째, 정치적 문제들은 일반적으로 법정 사건보다 더 복잡하다. 배심원들이 피고인이 범죄를 저질렀는지 여부를 판단할 수 있다 하더라도, 무엇이 최선의 사회, 경제, 이민 정책인지를 선택하는 것은 더 어렵다. 하물며 특정 정치인에게 투표하여 그의 공약집에 담긴 모든 정책을 동시에 선택하는 것은 훨씬 더 어려운 일이다.
이러한 복잡성은 민주주의 유권자들이 실제로 50% 이상의 확률로 최선의 선택을 할 수 있는지에 대한 의구심을 일으킨다. 이러한 문제는 해결하기가 훨씬 더 어려운데, 시민들이 이 모든 분야에 전문성을 갖추는 것은 현실적으로 매우 어려운 일이기 때문이다.[9]
마지막으로, 시민들이 독립적으로 투표를 하더라도 그들의 의사 결정 과정은 독립적으로 이루어지는 경우가 드물다. 법정에서는 배심원들이 가족과의 대화나 외부 뉴스 매체의 영향으로 편향된 판단을 내리지 않도록 주의를 기울인다.
하지만 민주주의에서는 이런 방식으로 개인들을 외부와 차단하는 것이 현실적으로 불가능하다. 더욱이, 이러한 [의사 결정 과정에서의 독립성의] 차이가 우리가 반드시 바로잡아야 할 문제인지도 분명하지 않다. 전체주의 체제는 시민들이 접하는 정치적 정보를 제한하는 것으로 악명 높은 반면, 민주주의는 자유로운 의견 교환을 장려한다는 점에서 높이 평가받는다.[10]
4. 결론
일부 철학자들은 콩도르세의 배심원 정리가 민주주의의 정당성을 뒷받침하는 근거를 제공할 수 있다고 주장해왔다. 콩도르세 정리의 전제 조건과 민주주의 사이에는 많은 차이점이 있다. 결국 이러한 차이점들에도 불구하고 민주주의가 여전히 대체로 최선의 선택을 할 것이라는 점을 보여주기 위해서는 추가적인 논증이 필요하다는 것이 분명해 보인다.
주석
[1] Marquis de Condorcet(1785) 참조.
[2] 콩도르세의 배심원 정리는 모든 배심원 결정에 적용되는 것은 아니다. 예를 들어, 미국의 형사 재판에서는 배심원들이 다수결로 결정을 내리는 것을 허용하지 않고, 만장일치로 최종 평결에 도달할 것을 요구한다. 또한 배심원들은 독립적으로 판단하지 않고 함께 협의하는 과정에서 자연스럽게 서로의 판단에 영향을 미친다.
[3] 이때 배심원들의 판단이 서로 독립적이라고 가정하고 있으므로, [각 경우가 발생할 확률을 구하려면] 각 경우에서 배심원들의 개별 확률(역주: 올바른 판단을 내릴 확률인 60% 또는 잘못된 판단을 할 확률인 40%)들을 단순히 곱하면 된다(예를 들어, [경우 1이 발생할 확률을 구하기 위한] 60% × 60% × 40%처럼). 그리고 다수가 올바른 평결을 내릴 최종 확률(64.8%), 즉 [다수가 올바른 평결을 내리는] 네 가지 경우 중 하나가 발생할 확률을 구하기 위해서는 네 가지 경우 각각의 확률(14.4%, 14.4%, 14.4%, 21.6%)을 더하면 된다. 이는 이 경우들이 상호 배타적이기 때문이다. 즉, 어떤 두 경우도 동시에 발생할 수 없는데, 각 경우가 나머지 세 경우와 함께 성립할 수 없기 때문이다. 더 자세한 내용은 Thomas Metcalf의 The Probability Calculus를 참조하라.
[4] 더 일반적으로, 다음 공식을 사용할 수 있다.
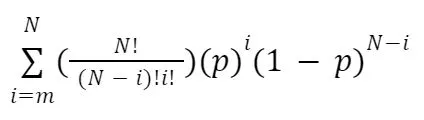
여기서 ‘N’은 투표자의 총 수, ‘m’은 과반수를 구성하기 위해 필요한 투표자 수, ‘p’는 개별 투표자가 올바른 결정을 내릴 확률이다.
[5] 배심원의 수와 능력 수준에 따라 다수결로 올바른 평결이 내려질 확률을 계산하려면 이 링크를 이용할 수 있다. 해당 사이트(Wolfram Alpha n.d.)에서는 배심원 총원은 ‘3’, 다수를 이루는 데 필요한 배심원 수는 ‘2’, 각 배심원이 올바른 평결을 내릴 확률은 ‘0.6’으로 이미 입력되어 있지만, 다른 계산을 위해 이 숫자들을 변경할 수 있다. 예를 들어, 각 배심원이 올바른 평결을 내릴 확률이 0.55이고, 배심원이 11명이며, 따라서 다수를 위해 6명이 필요한 경우, ‘3’을 ‘11’로, ‘2’를 ‘6’으로, ‘0.6’을 ‘0.55’로 바꾸면 된다.
[6] 이렇게 생각해 보자. 동전을 단 몇 번 던져 보는 것으로는 그 동전이 공정한지(역주: 앞면과 뒷면이 나올 확률이 같은지) 판단하기 어렵다. 처음 두 번 던졌을 때 모두 앞면이 나와 동전이 편향된 것처럼 보일 수도 있다. 그러나 공정한 동전을 던지는 횟수가 많아질수록, 앞면이 나오는 비율이 약 50%에 가까워질 가능성이 점점 더 커진다. 따라서 더 많이 던지는 것은 동전이 앞면이 나올 실제 확률을 드러내는 좋은 방법이다. 마찬가지로, 유권자들이 60%의 확률로 올바른 답을 선택한다면, 소수의 유권자만으로는 이를 확인하기 어려울 수 있다. 하지만 더 많은 유권자를 추가할수록 그들이 약 60%의 확률로 올바른 답을 선택하게 될 가능성이 높아지며, 이는 다수가 올바른 평결을 내리도록 이끈다.
[7] 민주주의 투표에서는 종종 두 개 이상의 선택지가 있다. 배심원 제도에서는 유죄와 무죄라는 단 두 가지 선택지만 있다. 하지만 투표소에서 유권자들은 여러 다른 정치인과 정책 중에서 선택해야 할 수도 있다. 이러한 차이는 보완할 수 있다. 가령 정부가 모든 투표에서 두 가지 선택지만 제공하도록 규정할 수도 있다. 또한 일부 철학자들은 콩도르세 배심원 정리가 여러 선택지가 있는 경우에도 작동할 수 있다고 주장한다. 유권자들이 최선의 선택지를 고를 확률이 다른 각각의 잘못된 선택지를 고를 확률보다 더 높기만 하면 된다. Goodin and List(2001)를 참조하라.
[8] 실제로 이 정리는 한 선택지가 어떤 특정 속성을 가지고 다른 선택지는 그렇지 않을 때, 그 특정 속성에 대해서도 적용된다. 예를 들어, 한 정치인이 다른 정치인보다 저소득층에게 더 많은 도움을 줄 것이고, 각 유권자가 저소득층을 더 많이 도울 정치인을 선택할 확률이 51% 이상이라면, 콩도르세 정리는 유권자가 더 많아질수록 유권자들이 저소득층을 더 효과적으로 도울 정치인을 선택할 가능성이 더 높아진다는 것을 보여준다.
[9] Thomas Metcalf의 Ethics and the Expected Consequences of Voting(번역본: 윤리학과 투표의 예상 결과)의 제4절, “Political Knowledge, Morality, and Blame”에서는 대부분의 미국인들이 정치 관련 지식이 상대적으로 부족하다는 증거를 간략히 검토한다. 대부분의 미국인들은 어떤 정책과 후보자가 가장 바람직한지를 판단할 만한 전문성이 매우 부족하다.
[10] 민주주의 옹호론 중 다양한 정치인과 정책을 지지할 이유들을 공유하고 토론하는 것에 중점을 두는 접근법에 대한 개관은 Min and Wong(2018)을 참조하라.
[역주1] 한국의 국민 참여 재판에서는 유무죄와 양형을 선고할 권한은 판사에게 있고 배심원은 판결을 권고할 수만 있다. 그러나 이와 달리 영미법 국가에서는 배심원들이 다수결로 피고인의 유무죄를 직접 결정하는 시스템을 채택하고 있다.
[역주3] 즉, 민주주의는 거의 항상 최선의 선택을 한다는 매우 강한 결론이 아닌 상대적으로 약한 결론을 도출하는
참고 문헌
List, Christian and Robert Goodin. (2001), “Epistemic Democracy: Generalizing the Condorcet Jury Theorem.” Journal of Political Philosophy 9(3): 277–306.
Marquis de Condorcet. (1785). Essay on the Application of Analysis to the Probability of Majority Decisions.
Min, John and James Wong. (2018). “Epistemic Approaches to Deliberative Democracy.” Philosophy Compass 13(6).
Wolfram Alpha. (N.d.). WolframAlpha. https://www.wolframalpha.com/
관련 에세이
Ethics and the Expected Consequences of Voting by Thomas Metcalf (번역본: 윤리학과 투표의 예상 결과)
Free Speech by Mark Satta (번역본: 언론의 자유)
John Rawls’s “A Theory of Justice” by Ben Davies
The Probability Calculus by Thomas Metcalf
저자 소개
웨스 시스코(Wes Siscoe)는 노터데임 대학교(the University of Notre Dame)의 ‘덕과 소명 프로젝트’(Virtues and Vocations project) 박사후연구원으로, 교수진이 덕 교육을 그들의 강의에 통합하도록 돕는 일을 하고 있다. 애리조나 대학교(the University of Arizona)에서 박사 학위를 받았다. 그의 연구는 합리성, 언어, 덕과 같은 여러 주제를 다루며, 이것들이 인간의 탁월성과 성취를 설명하는 데 있어서 갖는 중요성을 탐구한다. WesSiscoe.com
이 글은 Wes Siscoe의 Marquis de Condorcet’s Jury Theorem and Democracy을 번역한 것입니다.
1000-Word Philosophy 팀으로부터 허가를 받아 한국어 번역본을 게시합니다.
One thought on “콩도르세의 배심원 정리와 민주주의 – Wes Siscoe”
Comments are closed.